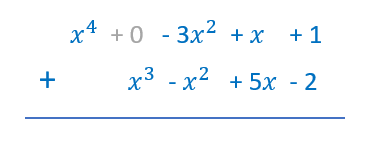OPERACIONES CON POLINOMIOS

            

Ley de los signos matemática, suma, resta, multiplicación y división

Los signos de matematicas conocidos como +, -, x y /, son simbolos aritmeticos para indicar el estado de una operación matemática. Este tipo de operaciones son conocidas como la adicion, sustraccion, multiplicacion y division. Así mismo también pueden englobar a los signos algebraicos en las operaciones.

La matemática es una de las ciencias que estudia todo lo relacionado con los números, figuras geométricas, símbolos y más. Las matemáticas se fueron creando con base a teorías, definiciones y leyes relacionadas entre sí. Es por ello que la mayoría de sus ideas fueron descubiertas de más de 4000 años. El desarrollo constante de la civilización ha sido en gran parte por las matemáticas y otras ciencias que se combinan.

Este tipo de ciencia es aquella que se encarga de descifrar y trabajar con elementos abstractos que estén relacionados entre ellos. Para ser utilizado se necesita el razonamiento lógico. Es por ello que su uso ha sido importante para el desarrollo en avances tecnológicos. Esta se divide en cuatros ramas como lo son la aritmética, álgebras, geometría y estadística. En la actualidad se utilizan las matemáticas como una herramienta para las vida cotidiana.

A pesar que se ha afirmado que en las matemáticas no existen leyes si se puede asegurar que existan normas o condiciones para poder realizar las operaciones sin ningún tipo de problema. En matemáticas existen leyes que se encargan de signos para realizar las operaciones más básicas como lo son suma, resta, división y multiplicación. Este tipo de ley es la que se ocupa del sentido de las operaciones, como se ejercen y la dirección de los signos. Es por ello que a continuación daremos un resumen de la ley de los signos de matemáticas

       

NOTA:EN LA SUMA Y RESTA SIEMPRE EL RESULTADO DE LA OPERACION TENDRA EL SIGNO DEL NUMERO MAS GRANDE

Ley de los signos de matemática

Dicha ley de los signos está basada en la multiplicación. Es decir se rige para que los números se multipliquen como corresponda. La ley se basa en lo siguiente: si los signos son iguales el resultado debe ser positivo. En cambio si los signos son diferentes el resultado será negativo. En otras palabras podría decirse signos iguales se suman, signos diferentes se restan. Esto va relacionado en operaciones básicas con números enteros. Es por ello que esta forma o ley se debe memorizar de una forma simple para realizar otro tipo de operaciones.

Como antes se mencionó la ley de los signos va a enfocarse en los signos + y -, que se denomina más o positivo y menos de negativo. En el caso de las operaciones de suma y resta de números enteros el resultado positivo será representado por el signo + y el resultado negativo por el signo –. Sin embargo para la multiplicación y división va a corresponder el positivo si los dos números son positivos y negativo si se encuentra un número positivo y otro negativo. Así mismo se puede observar en operaciones de ecuaciones algebraicas.

En general la ley de los signos está relacionada con el resultado de una operación entre números positivos y negativos. Es decir el resultado entre dos numero positivos será positivo. De igual forma se puede decir que el resultado entre un número positivo y negativo será negativo. Por otro lado dos números negativos tendrán por resultado un número positivo. A continuación representamos una fórmula para la ley de los signos.

(+) . (+)= (+) (el resultado de una operación dos números positivos es positivo)

(-) . (-)= (+) (el resultado de una operación número negativo y uno negativo es positivo)

(+) . (-)= (-) (el resultado de una operación número positivo y uno negativo es negativo)

(-) . (+)= (-) (el resultado de una operación número negativo y uno positivo es negativo)

Ley de los signos para suma

Para ello existen algunas reglas:

En suma de números positivos con números positivos, el resultado es un número positivo.

De ser una suma de un número negativo con otro número negativo, el resultado es negativo.

Si se trata de un número positivo con un número negativo el signo en el resultado es del número entero de mayor valor.

Nota: se debe tomar en cuenta que si un número no posee un signo evidente este se sobre entiende que es de signo positivo + y no es necesario escribirlo. En el caso de ser un resultado negativo, se necesita escribir el signo negativo.

Ejemplos:

4 + 8= 12

(-5) + (-6)= -11

-7 + 4= -3

Ley de los signos para resta

En este caso la ley aplica en el mismo sentido de la suma, poniéndose en práctica las mismas reglas.

(+6) – (+2)= +4

(-7) – (-4)= -3

Ley de los signos para multiplicación y división

Para estas operaciones también existen diversas normas muy parecidas a la suma

En el caso de multiplicar o dividir un signo positivo con otros positivo el resultado es positivo.

De multiplicar o dividir un signo negativo con otro negativo el resultado será positivo.

Por último si se multiplica o divide un signo negativo con uno positivo o viceversa siempre será negativos, sin tomar en cuenta el mayor valor del número.

(+6) ÷ (+4)= +1,5

(-8) ÷ (-4)= +2

(+4) ÷ (-2)= -2

Importancia de la ley de los signos

Como se mencionó anteriormente las matemáticas son realmente importantes como una herramienta para la evolución y creación de nuevos teoremas y más. En nuestra vida cotidiana se utilizan en un sinfín de situaciones como el administrar dinero, calcular distancias, y el razonamiento matemático.

Conocer con exactitud las matemáticas y aprender sus normas y leyes se trata de crear habilidades para resolver problemas importantes en la vida. Las matemáticas y todo lo que las relaciones como lo son sus leyes son relevantes para el desarrollo de un país, la innovación, vanguardia y exigencias económicas. El dominio de las matemáticas es una cuestión que tiene que ver con grandes aspectos de todo el mundo.

Las matemáticas en algunas ocasiones suelen ser un poco difíciles de entender. Sin embargo se debe tomar en cuenta que en el caso de la ley de los signos es una muy sencilla de aplicar y de aprender. Se trata de adquirir y poner en práctica conocimientos importantes que desde siempre son enseñados en cualquier nivel educativo. Es por ello que no se debe dejar a un lado este tipo de aprendizaje y aprovechar todo las clases y teorías relacionadas a las mismas.

 SUMA Y RESTA DE POLINOMIOS

Sumar o restar polinomios equivale a sumar o restar los monomios (del polinomio) semejantes dos a dos. Con un ejemplo lo veremos mejor. Si queremos sumar p ( x ) = x 2 − x + 1 y q ( x ) = 3 x 2 + x − 2 agrupamos los monomios semejantes dos a dos y operamos.

¿Qué son los polinomios?

Antes de empezar a aprender a sumar polinomios debemos saber qué son y qué propiedades tienen. Es importante entender cuál es la parte literal, el grado y saber ordenar sus términos.

Si todavía no tienes claro estos conceptos te invito a que leas los post anteriores sobre las propiedades de los monomios y las propiedades de los polinomios.

La suma se puede hacer de dos formas distintas: en horizontal y en vertical. Vamos a ver las dos maneras y después puedes elegir cuál te resulta más fácil utilizar.

Suma de polinomios en horizontal

Para hacer las operaciones en horizontal primero escribimos un polinomio y seguido en la misma línea escribimos el otro que vamos a sumar o restar. Después, agrupamos términos semejantes.

Ejemplo:

Vamos a realizar la suma. Para ello escribimos cada uno rodeado de paréntesis y con el signo de la suma entre ellos.

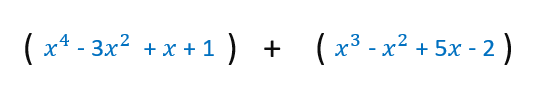
Fíjate en los términos que son semejantes entre los dos polinomios.

No podemos sumar dos términos que tienen distinto grado, solo podemos agrupar los que sean semejantes y después sumar.

En la siguiente imagen están identificados los términos semejantes rodeados con el mismo color.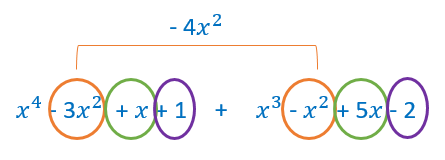

Igual que hemos hecho con el término de grado 2, debemos sumar los términos de grado 1 y los términos de grado 0.

El resultado de la suma es: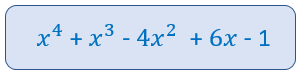

Suma de polinomios en vertical

Para hacer las sumas en vertical debemos escribir el primer polinomio ordenado. En el caso de que sea incompleto es conveniente dejar los huecos libres de los términos que falten. Después, escribimos el siguiente polinomio debajo del anterior, de manera que coincida justo debajo el término semejante al de arriba. Después, ya podemos sumar cada columna.

Ejemplo:

Vamos a ver la suma en vertical con los dos polinomios del ejemplo anterior.Fíjate en el primer polinomio. Hay que escribirlo ordenado y ver si está completo. En este caso falta el término de grado 3, entonces debemos dejar el hueco correspondiente o escribir un cero en su lugar.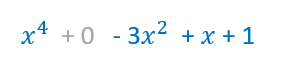Ahora escribimos el segundo debajo del primero, de manera que coincidan los términos semejantes uno debajo de otro.

Solo queda sumar cada columna, es decir,  sumar los términos semejantes.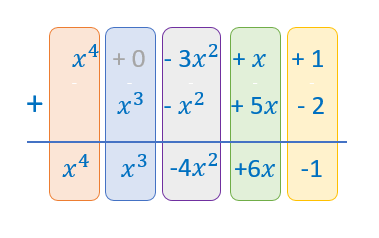Ya has aprendido a sumar polinomios de dos maneras diferentes: en horizontal y en vertical. ¿Cuál te ha parecido más sencilla?